
Now that
Fractint has switched the integer precision for the loop
iteration count to 32 bits, fractals can now iterate over 4 billion times
per pixel. Who can imagine wanting to? Well, I can!
At least some day.
 My most audacious attempt to date still has the puny limit
of 2 million iterations as a bailout value, but I am striving to find
interesting regions at higher and higher iteration levels.
I like to think of
it as a complimentary task to the
deep zooming side of fractint. While deep
zooming looks for fractal detail in areas that require more and more decimal
places to differentiate between adjacent pixels, high iteration fractals
require longer and longer iteration counts before the fractal detail will
emerge. Ultimately, both these techniques should be combined to push the
fractal explorations to there furthest reaches, but I have that selfish human
trait of wanting to see the results somewhere within a year, so I keep my
searches on the quick side of the cross over from floating point into
arbitrary precision math.
My most audacious attempt to date still has the puny limit
of 2 million iterations as a bailout value, but I am striving to find
interesting regions at higher and higher iteration levels.
I like to think of
it as a complimentary task to the
deep zooming side of fractint. While deep
zooming looks for fractal detail in areas that require more and more decimal
places to differentiate between adjacent pixels, high iteration fractals
require longer and longer iteration counts before the fractal detail will
emerge. Ultimately, both these techniques should be combined to push the
fractal explorations to there furthest reaches, but I have that selfish human
trait of wanting to see the results somewhere within a year, so I keep my
searches on the quick side of the cross over from floating point into
arbitrary precision math.
As well as the maximum iteration value, I think the minimum iteration value
for an image is equally interesting.
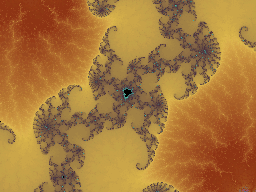
 This image, (which I call "Tapestry
" for obscure subconcious reasons that my therapist isn't telling me),
has a minimum iteration/pixel of 83,693.
Thats right! Every pixel in the image
looped at least that many times, while those at the mini-brot boundaries went
up to 2 million iterations. I find it incredible that this kind of detail and
beauty lay dormant, waiting, for that many iterations, before it decided to
unveil itself. At this scale, right down at the limits of ordinary floating
point precision, where the difference between one pixel and the next is
of the order of 1x10e-18, it is hard to imagine that these small variations
can
still result in a complex pattern such as this, but there it is. Furthermore,
all indications show that, things just get more complicated, more intricate,
the longer that you iterate. I like the texture invoked by the minute
detail of the image. It becomes so involved that there aren't enough pixels
on the screen to adequately represent it and the pattern becomes a mere
hint of what might be there.
This image, (which I call "Tapestry
" for obscure subconcious reasons that my therapist isn't telling me),
has a minimum iteration/pixel of 83,693.
Thats right! Every pixel in the image
looped at least that many times, while those at the mini-brot boundaries went
up to 2 million iterations. I find it incredible that this kind of detail and
beauty lay dormant, waiting, for that many iterations, before it decided to
unveil itself. At this scale, right down at the limits of ordinary floating
point precision, where the difference between one pixel and the next is
of the order of 1x10e-18, it is hard to imagine that these small variations
can
still result in a complex pattern such as this, but there it is. Furthermore,
all indications show that, things just get more complicated, more intricate,
the longer that you iterate. I like the texture invoked by the minute
detail of the image. It becomes so involved that there aren't enough pixels
on the screen to adequately represent it and the pattern becomes a mere
hint of what might be there.
So where do you look for this type of image? Well
anywhere approaching
the boundary of the Mandelbrot, or the boundary of any minibrot, you will find
the iteration count must be set higher and higher to resolve the detail.
 How much patience do you have? Compute times can become rather tedious when
you iterate this long, but the rewards are there for those who look.
How much patience do you have? Compute times can become rather tedious when
you iterate this long, but the rewards are there for those who look.
 It's just a search process of
ever lengthening intervals, to zoom in on these regions, pinpointing
areas of interesting detail. I like to jump from one region around a minibrot
into another region of the next minibrot as I zoom slowly into the Mset,
picking up characteristic detail from each level. The influence of each
minibrot I visit, is clearly evident in the hierarchy of detail that make
up the whole image. The colouring algorithm for the images on this page
uses the
log-palette option from the "X" menu of Fractint.
Can I say 'palettable' here without anyone groaning? Maybe not. Anyway,
I find that log palettes give the most suitable
distribution of colours across such a broad range of values. Other techniques
are certainly equally as valid. I just happen to have my artistic preferences.
These images are all from the mandelbrot, but the use of high-iteration
in other fractal formulae can give equally elaborate images.
It's just a search process of
ever lengthening intervals, to zoom in on these regions, pinpointing
areas of interesting detail. I like to jump from one region around a minibrot
into another region of the next minibrot as I zoom slowly into the Mset,
picking up characteristic detail from each level. The influence of each
minibrot I visit, is clearly evident in the hierarchy of detail that make
up the whole image. The colouring algorithm for the images on this page
uses the
log-palette option from the "X" menu of Fractint.
Can I say 'palettable' here without anyone groaning? Maybe not. Anyway,
I find that log palettes give the most suitable
distribution of colours across such a broad range of values. Other techniques
are certainly equally as valid. I just happen to have my artistic preferences.
These images are all from the mandelbrot, but the use of high-iteration
in other fractal formulae can give equally elaborate images.
You might ask me how I figured out the minimum iteration value for these images.
Well it isn't too complicated. One of Fractint's features when using
log-palette mode, is an auto-detect function.
 If you are in the Basic
Options Menu "X", scan down the left column until you see
the Log Palette selection. One of the options in this mode is 2
which puts it in auto mode. When you go back to recalculate your image, you
will notice that the first thing Fractint does, is to trace the entire
border of the image. This may be very quick or it may take some time to
complete. What it is doing is looking for the lower limit for an iteration
count. This works very well in the Mandelbrot because the set is connected,
with no internal local minima and the lowest iteration count will always be
somewhere on the image boundary. This certainly
isnt' true for all fractal types however, so be careful how you use this.
Once it has found this value and started
it's standard image calculation, a trip back to the Basic Menu will
show this number set to the lowest iteration value that it found.
If you are in the Basic
Options Menu "X", scan down the left column until you see
the Log Palette selection. One of the options in this mode is 2
which puts it in auto mode. When you go back to recalculate your image, you
will notice that the first thing Fractint does, is to trace the entire
border of the image. This may be very quick or it may take some time to
complete. What it is doing is looking for the lower limit for an iteration
count. This works very well in the Mandelbrot because the set is connected,
with no internal local minima and the lowest iteration count will always be
somewhere on the image boundary. This certainly
isnt' true for all fractal types however, so be careful how you use this.
Once it has found this value and started
it's standard image calculation, a trip back to the Basic Menu will
show this number set to the lowest iteration value that it found.
Back to The Fractint Home Page. or back to The Fractint Index Page.